Computational Fluid Dynamics

Biomembranes

When lipid molecules are immersed in an aqueous environment they aggregate spontaneously into a bilayer or membrane that forms an encapsulating bag called vesicle. This happens because lipids consist of a hydrophilic head group and a hydrophobic tail, which isolate themselves in the interior of the membrane. Because lipid membranes are ubiquitous in biological systems, an understanding of vesicles provides an important element to understand real cells.

Deformation of an ellipsoid membrane (top) to its energetic equilibrium: the red blood cell shape (bottom).

Phenomenological and rigorous continuum mechanical approaches agree that the membrane is endowed with a bending or elastic energy. Moreover, if the temperature and osmotic pressure of the vesicle do not change, the enclosed volume and surface area can be assumed to be conserved. The former is a consequence of the impermeability of the membrane. The latter is because the number of molecules remains fixed in each layer and the energetic cost of stretching or compressing the membrane is much larger than the cost of bending deformations.

The boundary condition couples the effect of the fluid to the force coming from the membrane. The latter consists in a nonlinear forth order operator defined on the moving membrane. Adaptive parametric finite element methods (AFEM) are invoked and studied in this project. In particular, due to geometric inconsistency, intriguing numerical artefacts take place when refining an a-priori unknown surface.

Local Researchers: A. Bonito and M.S. Pauletti.
External Collaborator: R.H. Nochetto (UMD).

Coupled Free and Porous Media Flows

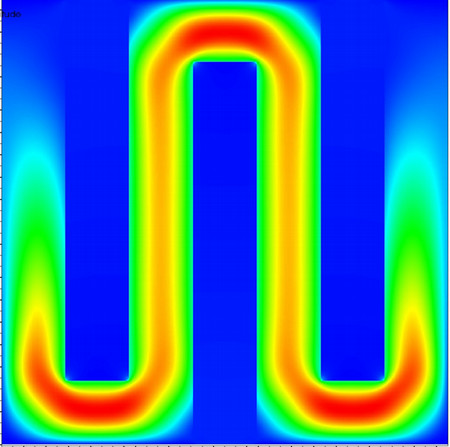
The flow through an idealized catalyzer. While most of the flow follows the channel, some is pressed through the porous walls and interacts with the catalyzing material.

The coupling of free flow with porous media flow appears in environmental applications, for instance when the transport of a pollutant from a river into the ground water is modeled, as well as in technical applications to filters and catalyzers. Due to different length and time scales in the free and porous subregions, respectively, this coupling can prove numerically challenging.

At Texas A&M, we address these challenges on two fronts. First, we are using mimetic finite element methods to obtain consistent discretizations in order to avoid mass loss at the interface. Second, we develop iterative solvers for the coupled problems, where standard methods fail due to the scale separation.

Local Researchers: G. Kanschat, R. Lazarov, J. Willems.
External Collaborators: O. Iliev (FTWM Kaiserslautern, Germany), B. Rivi�re (Rice University), B. Wohlmuth (Universit�t Stuttgart, Germany)

Incompressible Navier-Stokes

The research activity covered by this item ranges from the analysis of theoretical aspects of the incompressible Navier-Stokes equations to the analysis of various approximation techniques.

Kinetic energy in Taylor-Couette dynamo (Re=120, Rm=240).

The Navier-Stokes equations model the dynamic of incompressible viscous fluids. These equations play an important role in many academic fields (astrophysics, biology, mathematics, etc.) and engineering fields (aerospace, automobile, civil engineering, petroleum, nuclear, etc.). For instance these equations are used in weather prediction.

An important mathematical question regarding these equations is that of the existence of smooth solutions for long time in three space dimensions. This question is believed to be linked to what in the everyday life we observe as turbulence. Some of the faculty involved in this project focus their research activity on the smoothness and turbulence question.

Solutions to the Navier-Stokes equation must be approximated numerically.

Flow in a cavity composed of half a cylinder at Re=1000.

This task usually requires enormous computing power. New algorithms must be developed to minimize the computational cost of evaluating approximate solutions.

Local Researchers: J.-L. Guermond

Magneto-Hydro-Dynamic

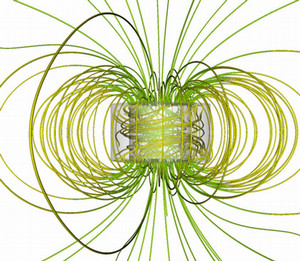
The problem under consideration is the so-called Dynamo problem. In astrophysical situations like stars or planets with a liquid core, a magnetic field is sustained by nonlinear interactions with large-scale movements of a conducting fluid.

Dynamo action in the von Karman Sodium Experiment

The fluid may be plasma in the stellar case, molten iron in the planetary case, or liquid gallium or sodium in experimental setups that try to reproduce the dynamo effect. One important aspect of the problem is that the magnetic field develops in an inhomogeneous medium: there are conducting regions and insulation regions.

The objective of this project is to contribute to the understanding of the mechanisms at the origin of the Geodynamo. Earth has a soft iron core surrounded by semi-liquid materials from the mantle that move around the core. It is believed that the magnetic field around the Earth is generated by large scale convective movements of the semi-liquid mantel, but it is not yet clear why the dynamo has a dipolar structure aligned with the Earth's rotation axis and why the dipole intermittently reverses polarity.

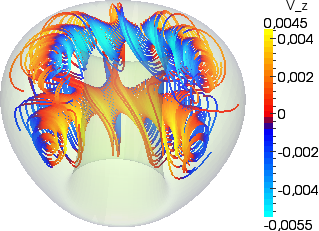
We are developing a 3D parallel code, called SFEMaNS, specialized to axi-symmetric geometries. We use Lagrange finite elements in the meridian section and Fourier expansions in the azimuthal direction.

Image: Streamlines for Lundquist number 226 in ITER-like configuration.

The code can handle highly heterogenous coefficients, including zero electric conductivity. The coupling between the various heterogenous sub-domains is done using an interior penalty technique. Parallelism is done with respect to the Fourier modes. SFEMaNS will be publicly available when the complete documentation is written (end of 2014?).

As SFEMaNS progresses and becomes more flexible, we expand our investigations beyond the Geodynamo. We are currently exploring the so-called reversed field pinch mechanism in plamsas (see panel), the Tayler instability in liquid metal batteries, and other MHD mechanisms involving two-fluid flows.

The team working on this project is composed of researchers from Texas A&M (USA), and Paris XI University (France).

Local Researcher: J.-L. Guermond,
External Collaborators: C. Nore (LIMSI/PXI, France), J. Leorat (Obs. Meudon, France), Wietze Herreman(LIMSI/PXI, France), Loic Cappanera (LIMSI, Orsay), Daniel Castanon (TAMU)

Nonlinear Conservation Laws (Entropy Viscosity Method)

Conservation equations are fundamental equations of physics expressing conservation of mass, momentum, and energy.

Mach 3 wind tunnel. Density. P1 finite elements

These equations are nonlinear and when viscous dissipation is negligible, the solutions develop shocks in finite time. The inviscid Burgers equation is the scalar prototype of these equations.

Standard approximation techniques based on non-viscous centered differencing usually fail on this type of problem: they are not dissipative and thus cannot dampen spurious oscillations generated by shocks and sharp gradients.

Mach 10 double Mach reflection. Density. P1 finite elements

The classical remedy consists of upwinding the approximation of space derivatives or to use Godunov type methods (which is essentially equivalent to upwind).

Since the pioneering work H. Nessyahu and E. Tadmor, it is now known that centered differencing methods can correctly approximate nonlinear conservation equations when supplemented with the right viscous dissipation. The key question is to come up with the right dissipation.

Rotating composite wave. P2 finite elements

This project aims at developing new numerical techniques for solving nonlinear conservation laws based on centered differencing. The key idea is to use the entropy equation to construct a nonlinear viscosity to dissipate energy in shocks and dampen spurious solutions. We call this method the Entropy Viscosity Method. Numerical experiments and theoretical considerations show that this approach is efficient and works with finite elements on non uniform mesh (triangles, quadrangles), spectral elements, and Fourier expansions.

Local Researchers: J.-L. Guermond, B. Popov, M. Nazarov
External Collaborators: R. Pasquetti (J. Dieudonn�, Univ. Nice, France)

Viscoelastic Fluids

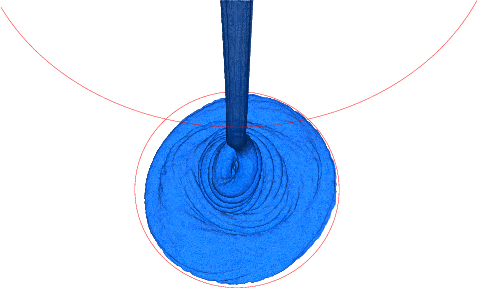
Viscoelastic flows with complex free surfaces are considered.

Buckling of a Newtonian Jet (view from top).

Such flows are involved in several industrial processes involving paints, plastics, food or adhesives but also in geophysical applications such as mud flows or avalanches.

Viscoelastic fluids are viscous fluids having elastic properties. They cannot be described with the classical theories of fluid or continuum mechanics. Additional laws have to be added in order to relate the stress to the velocity, this being the scope of rheology. Theoretical and computational aspects are investigated.

Buckling of a Viscoelastic Jet (view from top). Bonito, Picasso and Laso (2006).

A volume fraction of fluid method is used to describe the complex free surface.Hence, using an operator splitting method, the numerical methods consists in two steps. The prediction step consists in solving convection problems including the volume fraction of liquid dynamic. The correction step consists in solving a viscoelastic flow problem (either macroscopic or mesoscopic) without convection in a prescribed domain.

Local Researchers: A. Bonito.
External Collaborators: E. Burman (Sussex), Ph. Cl�ment, M. Laso (Madrid), A. Lozinski (Toulouse), Th. Mountford (EPFL), and M. Picasso (EPFL).

Flows in heterogeneous highly porous media

Flows in porous media appear in many industrial, scientific, engineering, and environmental applications. One common characteristic of these diverse areas is that porous media are intrinsicly multiscale and typically display heterogeneities over a wide range of length-scales.

Depending on the goals, solving the governing equations of flows in porous media might be sought at:

A coarse scale (e.g., if only global pressure drop for a given flow rate is needed, and no other fine scale details of the solution are needed).
A coarse scale enriched with some desirable fine scale details.
The fine scale (if computationally affordable and practically desirable).

At pore level slow flows of incompressible fluids through the connected network of pores are governed by Stokes' equations. On a field level fluid flows in porous media have been modeled mainly by mass conservation equation and by Darcy's law between the macroscopic pressure and velocity.

In naturally occurring materials, e.g. soil or rock, the permeability is small in granite formations, medium in oil reservoirs, and large in highly fractured or in vuggy media. The latter is characterized by a high porosity. Aside from these examples from hydrology and geosciences there are also numerous instances of highly porous man-made materials, which are important for the engineering practice. These examples include mineral wool with porosity up to 99.7%, industrial foams with porosity up to 95%, some bones, etc. In order to reduce the deviations between the measurements for flows in highly porous media Brinkman introduced a new phenomenological relation between the macroscopic velocity and the macroscopic pressure gradient - called Brinkman's law .

Solving the corresponding equations in highly heterogeneous media is a computationally intensive task. In this project we consider numerical methods and solution techniques for porous media flows in both Brinkman and Darcy regimes.

We have derived, studied, implemented, and tested:

a unified framework of the subgrid method for both Darcy's and Brinkman's problem that model flows in highly heterogeneous porous media;
a subgrid based two level domain decomposition preconditioner for solving both Brinkman and Darcy problems in highly heterogeneous porous media at the fine scale (often called iterative upscaling).

Local Researchers: Y. Efendiev, G. Kanschat, R. Lazarov, and J. Willems.
External Collaborator: O. Iliev (ITWM, Germany).